As of today, two competing scenarios exist to explain recent sub-millimeter observations of transitional disks with azimuthally extended non-axisymmetric brightness distribution. The accepted explanation for the observed asymmetries is the accumulation of dust grains in pressure maxima, in the core of vortices. These dust traps can be the very places where planets and planetary cores can be quickly assembled in the core-accretion scenario. We investigating these scenarios in order to test their viability. In (Regaly et al. 2012) we found that the dead zone model can successfully explain the observed large-scale asymmetries in three transitional diks (LkHα-330, SR 21N, and HD 1353444B). We investigated whether or not we can infer the formation mechanism (gap vs. dead zone) of the vortex from the morphology of the disk as seen in sub-millimeter ALMA observations in (Regaly et al. in prep). We concluded that the formation process of vortices can be inferred by analyzing the brightness morphology in high-resolution ALMA images. Recently, we investigated the effect of disc self-gravity on vortices formed at dead zone outer edges (Regaly et al. 2017).
Possible planet-forming regions on submillimetre images
|
Submillimetre images of transition discs are expected to reflect the distribution of the optically thin dust. Former observation of three transition discs LkHα-330, SR 21N, and HD 1353444B at submillimetre wavelengths revealed images which cannot be modeled by a simple axisymmetric disc (Brown et al. 2009). See an example image of SR 21N made at 880 μm by SMA radio telescope (upper figure). We have shown that a large-scale anticyclonic vortex that develops where the viscosity has a large gradient (e.g., at the edge of the disc dead zone), might be accountable for these large-scale asymmetries. |
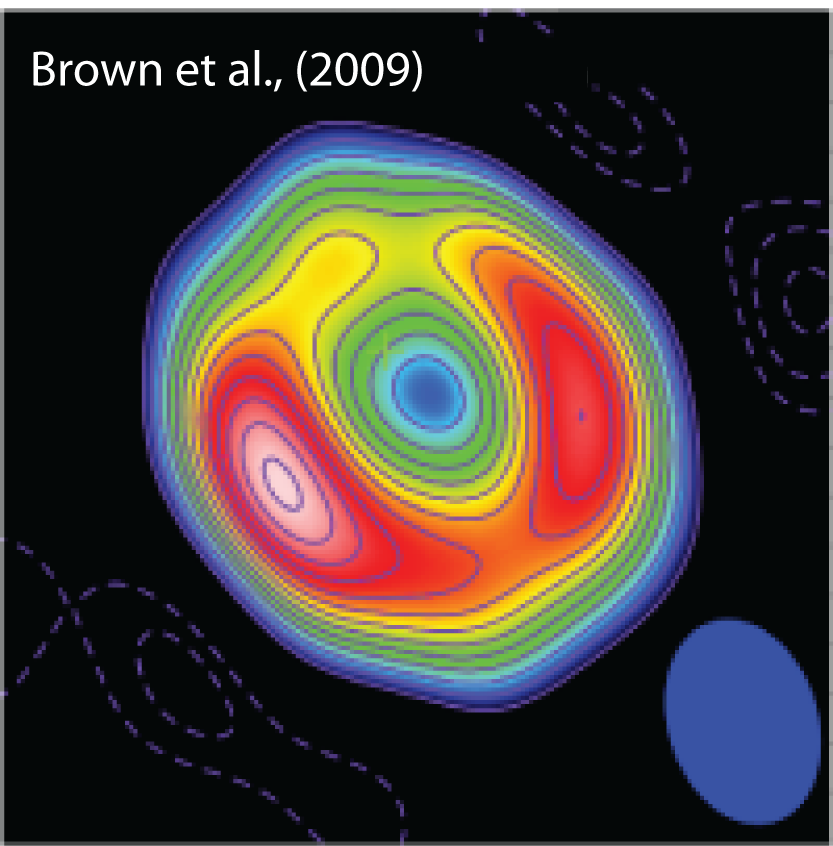 SMA image of SR 21. 
SMA image of SR 21 |
|
We modeled the long-term evolution of vortices being triggered by the Rossby wave instability. We found that a horseshoe-shaped (azimuthal wavenumber m=1) large-scale vortex forms by coalescing of smaller vortices within 5⋅10^4yr, and can survive on the disc life-time (∼ 5⋅10^6yr), depending on the magnitude of global viscosity and the thickness of the viscosity gradient. The two-dimensional grid-based global disc simulations with local isothermal approximation and compressible-gas model have been done by the GPU version of hydrodynamic code FARGO (GFARGO). The numerical simulations have been made on NVIDIA GTX 285 GPU cards. |
|
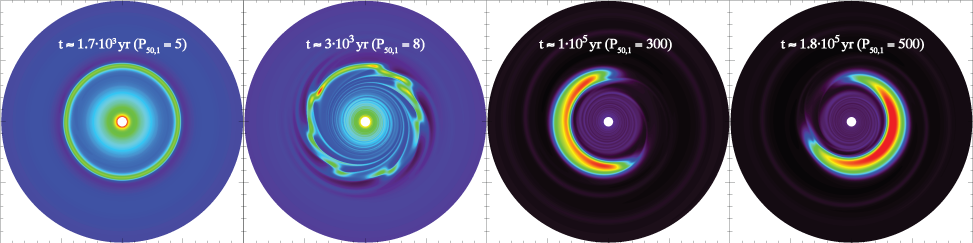
Vortex formation and coalescing revealed by numerical simulations with GFARGO. |
|
|
In order to show the resemblance of the observations of Brown et al. (2009) and signatures of large-scale Rossby-vortices in protoplanetary discs, we calculated submillimetre images using the 3D radiative transfer code RADMC-3D. First, the temperature structure of the disc was determined in a Monte Carlo simulation then the images at 340GHz (880 μm) were calculated via raytracing. Submillimetre Array (SMA) observations were simulated in the Common Astronomy Software Applications package (CASA). We also calculated SED from our synthetic disc model for all three sources and compared them to the observations (see an example for the case of SR 21). The SEDs calculated from our disc models match the observations shortwards of about 1 μm and longwards of about 10 μm. Between 1 and 10 μm, however, our models under predict the observed fluxes, which is a natural consequence of neglecting the inner disc emission. |
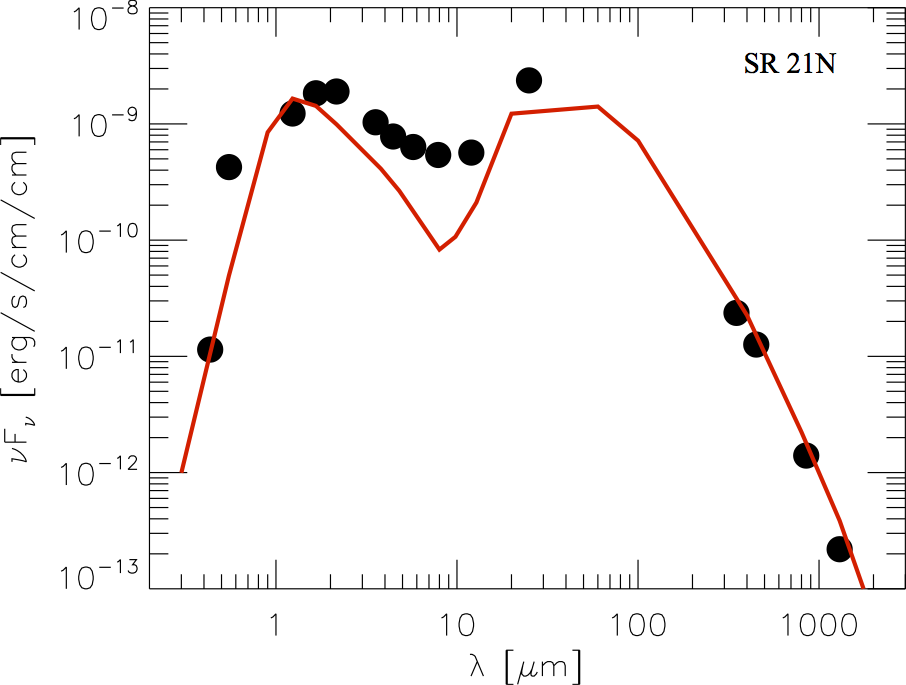 The observed (black dots) and the theoretical SEDs of SR 21N. 
The observed (black dots) and the theoretical SEDs of SR 21N. |
| By the striking similarities of the calculated and observed submillimetre images (for an example of that, see the synthetic image for the case of SR 21), we suggest that the three transition discs can be modeled by a disc possessing a large-scale vortex formed near the disc dead zone edge. Since the larger dust grains (larger than mm in size) are collected in these vortices, the non-axisymmetric submillimetre images of the above transition discs might be interpreted as active planet and planetesimal forming regions situated far (> 50 AU) from the central stars. Note that there exist further examples of discs showing non-axisymmetric submillimetre images, such as LkCa 15 (Pietu et al. 2006), GM Aur (Hughes et al. 2009), SR 24S (Andrews et al. 2010), and J1604-2130 (Williams & Cieza 2011) for which the same phenomenon might be responsible. |
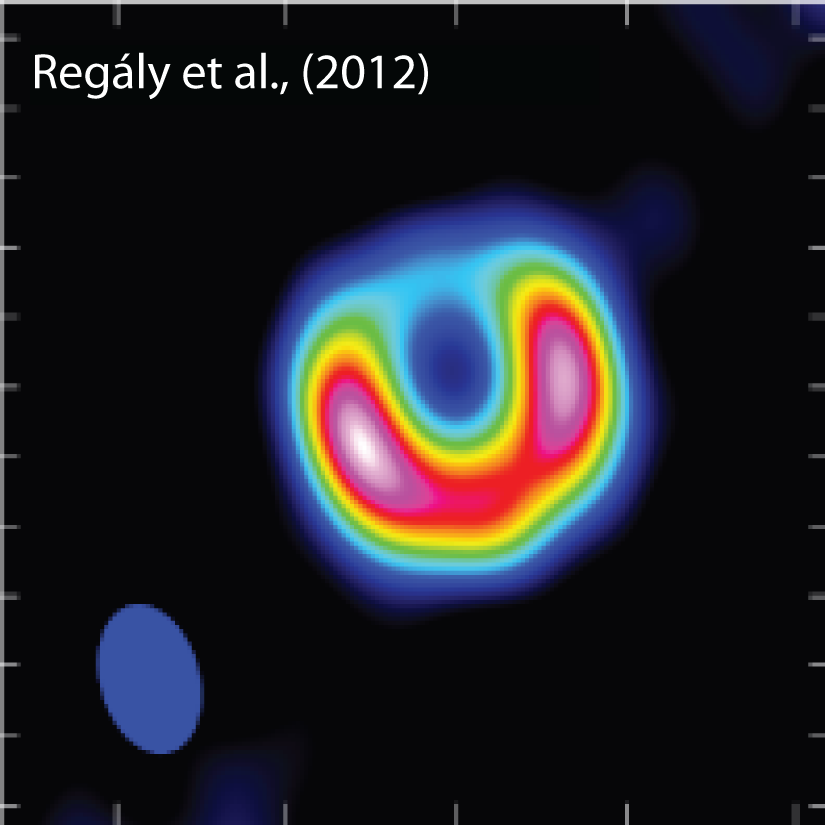 Submillimetre image of SR21N calculated by the 3D radiative transfer code. 
Submillimetre images of SR21N calculated by the 3D radiative transfer code. |
Appeared in Regály, Zs.; Juhász, A.; Sándor, Zs.; Dullemond, C. P., 2012, MNRAS, Volume 419, Issue 2, p1701
ADS:2012MNRAS.419.1701R,
arXiv:1109.6177
Interpreting Brightness Asymmetries in Transitional Disks
Vortex at Dead Zone or Planet Carved Gap Edges?
|
Protoplanetary discs, the remnant material of star formation are expected to have axisymmetric density distribution due the impulse momentum conserving contraction of the primordial gas cloud. In the contrary, submillimetre observations of transition discs (protoplanetary discs that are 1-Myr old and have significant gas content) taken in the recent years revealed non-axisymmetric brightness distribution for more than a dozen cases: RXJ-1604 (Mathewsetal. 2012); MWC-758 (Isella et al. 2010; Andrews et al. 2011); SAO-206462 (HD-135344B) and SR-21 (Brown et al 2009; Andrews et al. 2011; Pérez et al. 2014); DoAr-44 (Andrews et al. 2009, 2011); GM-Aur (Hughes et al. 2009; An- drews et al. 2011); LkCa-15 and RXJ-1615, UX-TauA, DM-Tau, WSB-60, DoAr-44, and UX-TauA (Andrews et al. 2011); LkHα-330 (Brown et al. 2008; Andrews et al. 2011); RXJ-1633 (Cieza et al 2012); V4046-Sgr (Rosenfeld et al. 2013); SR-24S (Andrews et al. 2010, 2011); HD 142527 (Fukagawa et al. 2013; Casassus et al. 2013); Oph IRS 48 (van der Marel et al. 2013); AB Aur (Tang et al. 2012; ?).. Since these disks are optically thin in the continuum, their sub-millimetre images reflect the distribution of the sub-millimeter sized dust particles (dynamically coupled to the gas) which are subject to accumulate in regions where the gas is accumulated and pressure enhancement occurs (Varniere & Tagger (2006), Terquem (2008). Two competing explanation exist as of today, which are common in the assumption of the origin of large-scale density asymmetry caused by vortices. |
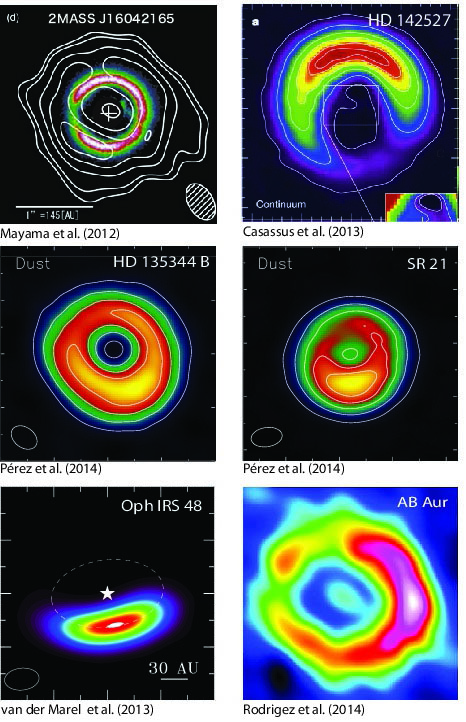 Transitional disks shwing large-scale asymetries. 
Asymmetric transitional disks. |
|
It is known that if Rossby wave instability (RWI) is excited, anticyclonic vortices form, which are subject to coalescing and a large-scale vortex develops. In protoplanetary diks, RWI can be excited at the edges of a gap opened by an embedded giant planet (Li et al. 2005). RWI can also be excited at the edges of the disc’s dead zone, an accretionaly inactive, low viscosity region developed due to the disc self-shielding against ionization radiation, if the radial extension of the region where the viscosity drops (i.e., the thickness of the dead zone edge) is small enough. In both scenarios, several anticyclonic vortices can be formed and coalesced to one large-scale vortex (see e.g., Regaly et al. (2012). |
|
|
We studied both vortex formation mechanisms by means of 2D locally isothermal hydrodynamical simulations of disks with α-type viscosity using the GPU-based FARGO code (Masset 2000). We modeled 1) the vortex formation at the edges of a giant planet (Rp=10AU, Mp/M✭=5×10−3) carved gap in three different viscosity regimes (α=10^−3, 10^−4, 10^−5), and 2) the vortex formation in a disk that has a sharp dead zone edge. In the dead zone model the value of α was smoothly reduced to 1% of its original value at distance of Rdze=12AU within ΔRdze=1Hdze and 1.5Hdze dead zone edge width. |
|
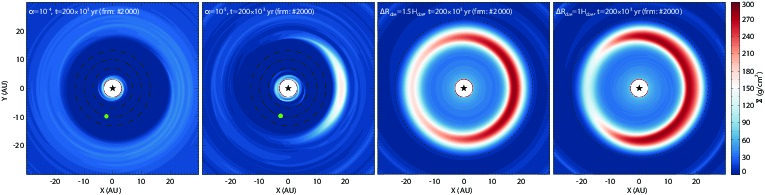
Density snapshots of hydrodynamic simulations taken at the end of the simulations. two left panels: GAP models with a 5 Jupiter mass giant planet with α = 10^-4 and 10^-5. two right panels: DZE models (α = 0.01, δα = 0.01, Rdze = 12AU) assuming ∆Rdze = 1.5 and 1Hdze. |
|
|
We observed that, the vortex vanishes by ∼300, 3000 orbits (which correspond to ~10^3 and 10^4 yr in our model) of the planet for α=10^−3, 10^−4, respectively. This transient nature of the vortex is in agreement with previous studies of Ataiee et al. (2013), and Fu et al. (2014). In contrast, the vortex survives up to the end of the simulations (6350 orbits, corresponding to 200⋅10^5 yr) for a nearly inviscid (α=10^−5) GAP and in DZE models. The gradient in the azimuthally averaged radial density profile is too shallow in viscous (α>10−5) GAP models, while steep enough in nearly inviscid GAP model and in DZE models to excite RWI (see Figure on the right). |
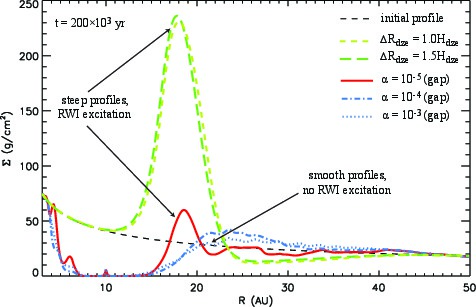 Radial density profiles averaged azimuthally. 
Radial density profiles. |
|
The azimuthal contrast in the density profile averaged over the extent of the vortex is high (∼12) in the inviscid GAP models, while low (1.5--3) in DZE models. The density enhancement is azimuthally as well as radially wider in DZE than in GAP models. It is also appreciable that the density enhancement is azimuthally more extended in DZE models than in GAP models. Although the density enhancement in the radial direction in the DZE models exceed that of in GAP models, and the vortex is spatially more extended in DZE models, the azimuthal contrast in gas density could be much higher in GAP models. |
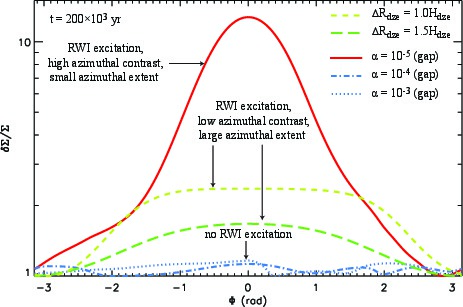 Radially averaged azimuthal profiles. 
Radially averaged azimuthal profiles. |
|
To create synthetic images first the output of the FARGO simulations were fed into the 3D radiative transfer code RADMC-3D (Dullemond et al., in prep) to calculate the dust temperature structure. We assumed a constant gas-to-dust ratio of 100 and a power-law grain size distribution between 0.1μm and 1000μm with a power exponent of -3.5. The dust is depleted completely inside the planetary orbit in the gap models, and inside the vortex. This dust clearing assumption is based on our simple 1D dust transport model that show very fast (1-2x105 yr) accumulation in density enhancements Then images were calculated at 880μm at inclination angles of 30 and 60 deg. ALMA observations were simulated using the Common Astronomy Software Applications v4.2. The simulated observations contained thermal noise with a precipitable water vapor column of 1.3 mm. We used three different antenna configurations for the full baseline array resulting in spatial resolutions of 0.1", 0.05" and 0.025", respectively. We used the full 7.5GHz bandwidth and the duration of the observations was set to 4 hours |
|
|
Brightness asymmetries, caused by the vortex are clearly visible in the images at all simulated spatial resolutions for both the GAP and DZE models. The azimuthal contrast in ALMA images is severely reduced at low spatial resolutions (0.1", 0.05") in the GAP models, due to beam dilution, compared to the contrast derived from the hydrodynamical frames. However, in DZE models the azimuthal contrast is insensitive to spatial resolution in the tested range. The inner edge of the gap appears to be eccentric in the GAP models, due to beam convolution effects at low spatial resolutions. |
|
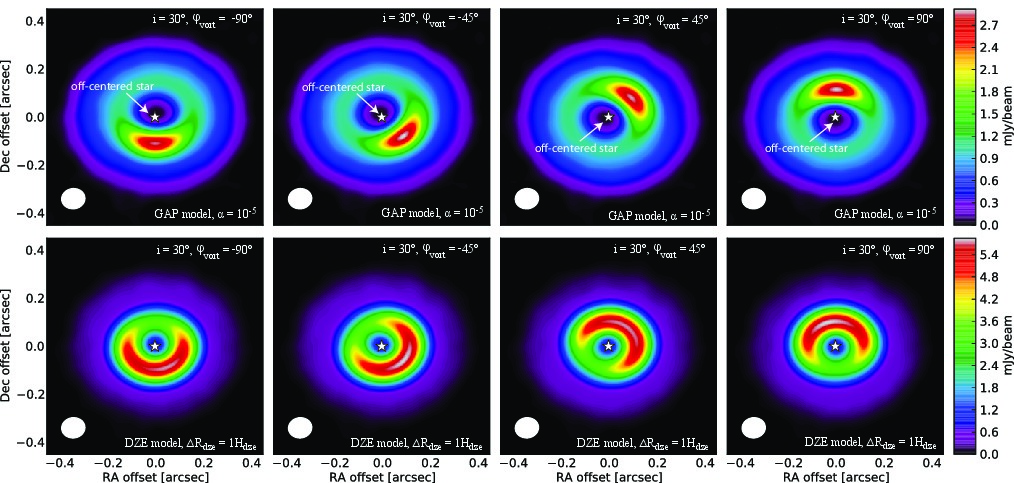
Synthetic ALMA images in GAP (upper row) and DZE (lower row) models with low resolution (0.1"). |
|
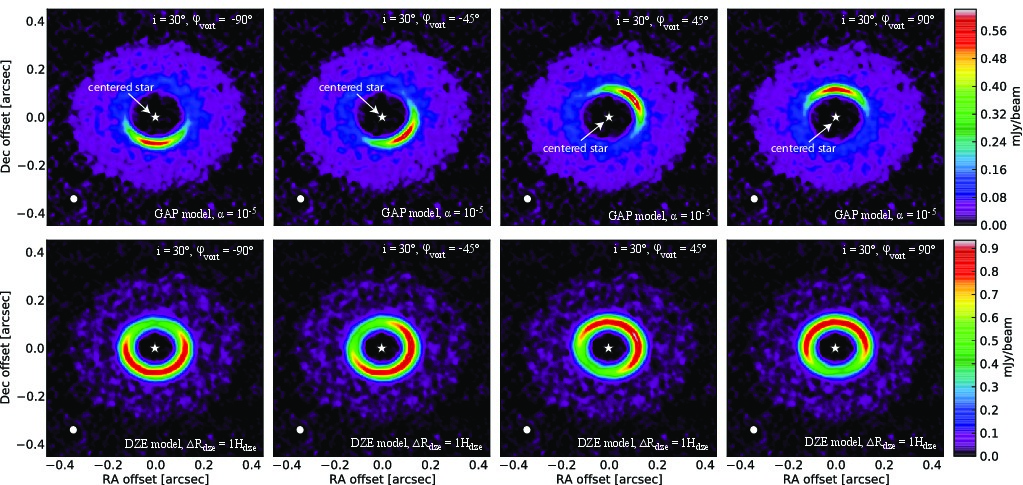
Synthetic ALMA images in GAP (upper row) and DZE (lower row) models with high resolution (0.025"). |
|
|
Due to the low azimuthal contrast in DZE models, the vortex splits into two separated blobs in low-resolution images, if the disk is seen in high inclination angle, e.g. 60 deg. In contrast, the vortex is well defined in GAP model due to the high azimuthal contrast. | |
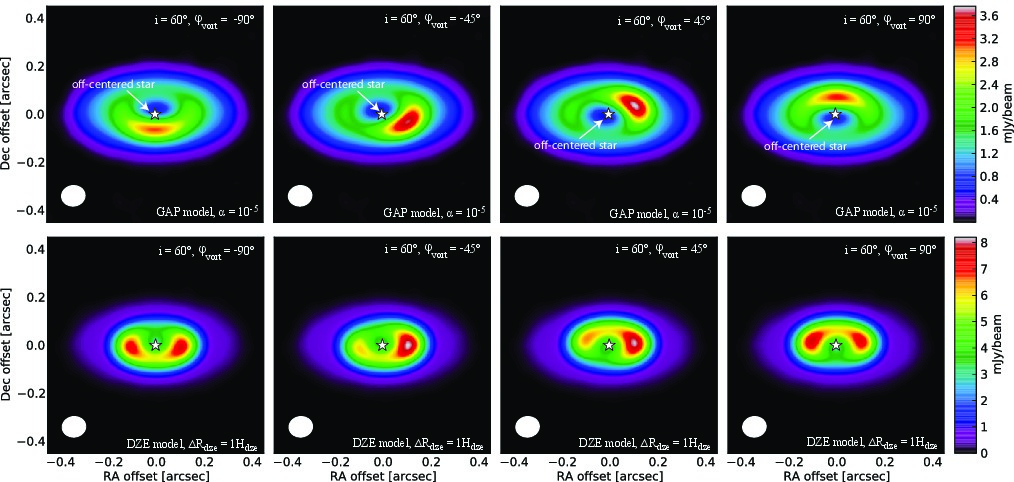
Synthetic ALMA images in GAP (upper row) and DZE (lower row) models with low resolution (0.1"). |
|
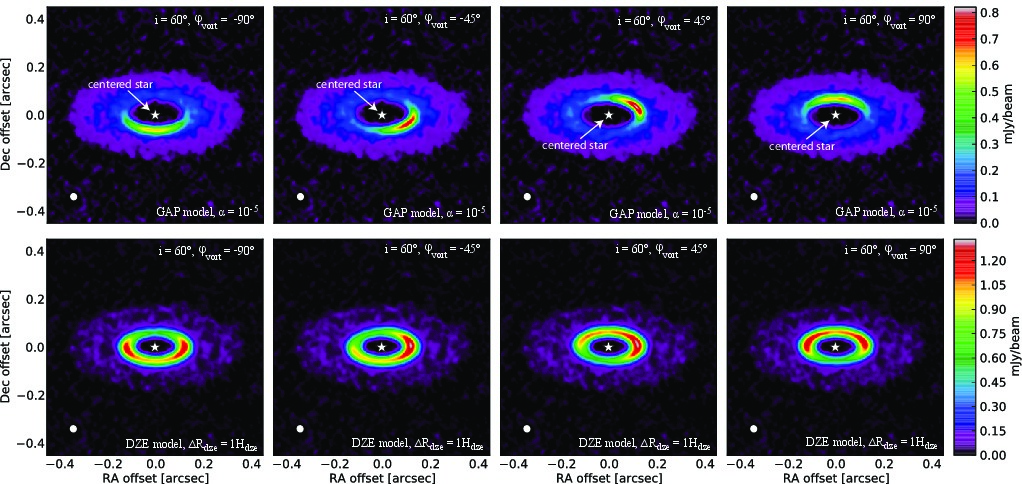
Synthetic ALMA images in GAP (upper row) and DZE (lower row) models with high resolution (0.025"). |
|
|
Vortices excited at the gap edge carved by a giant planet have a different morphology compared to that of vortices excited at the dead zone outer edge. Vortices at gap edges are azimuthally more compact and have higher azimuthal contrast than their counterparts at the edge of a dead zone. It is thus possible to infer the excitation mechanism of such vortices by studying the shape and the contrast of surface-brightness asymmetries in sub-millimeter, especially in ALMA observations. One needs, however, a spatial resolution that is similar to or higher than the radial extent of the vortex to measure the true contrast between the vortex and the background disk. At lower spatial resolution the observed contrast can be severely lowered by beam-dilution. |
|
In preparation, Regály, Zs.; Juhász, A.; Tarczay-Nehéz, D.
Conference poster Planet Formation and Evolution, Kiel, 2014: download (A3)
Vortex stretching in self-gravitating protoplanetary discs
|
Horseshoe-shaped brightness asymmetries of several transitional discs are thought to be caused by large-scale vortices. Anticyclonic vortices are efficiently collect dust particles, therefore they can play a major role in planet formation. Former studies suggest that the disc self-gravity weakens vortices formed at the edge of the gap opened by a massive planet in discs whose masses are in the range of 0.01≤M<disc/M*≤0.1. We investigated the long-term evolution of the large-scale vortices formed at the viscosity transition of the discs' dead zone outer edge by means of two-dimensional hydrodynamic simulations taking disc self-gravity into account. |
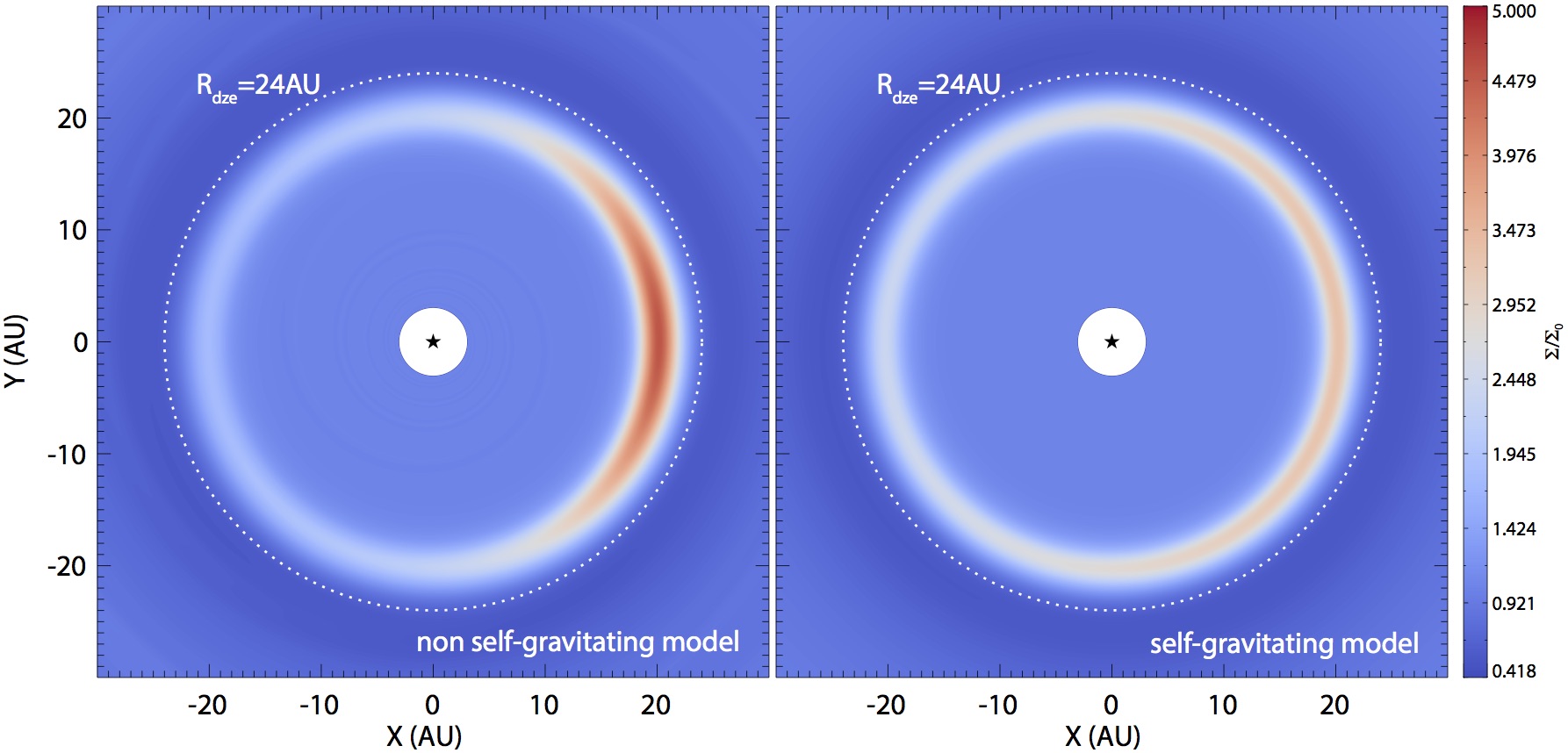 Non self-gravitating and self-gravitating vortices 
|
|
We perform a numerical study of low mass, 0.001≤Mdisc/M*≤0.01, discs, for which cases disc self-gravity was previously neglected. The large-scale vortices are found to be stretched due to disc self-gravity even for low-mass discs with Mdisc/M*≥005 where initially the Toomre Q-parameter was ≲50 at the vortex distance. As a result of stretching, the vortex aspect ratio increases and a weaker azimuthal density contrast develops. The strength of the vortex stretching is proportional to the disc mass. The vortex stretching can be explained by a combined action of a non-vanishing gravitational torque caused by the vortex, and the Keplerian shear of the disc. Self-gravitating vortices are subject to significantly faster decay than non-self-gravitating ones. We found that vortices developed at sharp viscosity transitions of self-gravitating discs can be described by a GNG model as long as the disc viscosity is low, i.e. αdz≤10-5. |
|
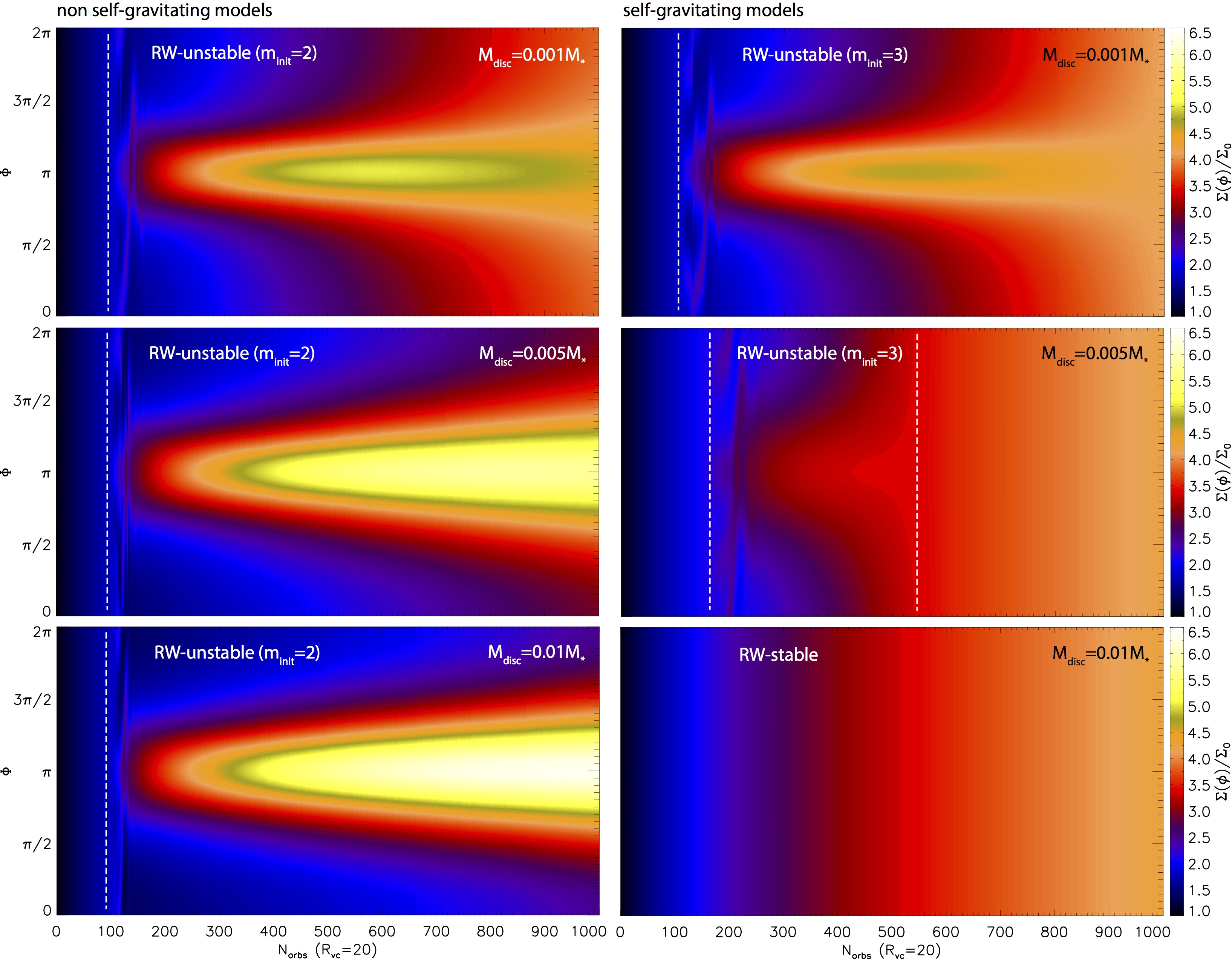 Vortex evolution in models assuming viscosity of αdz10-4. 
|
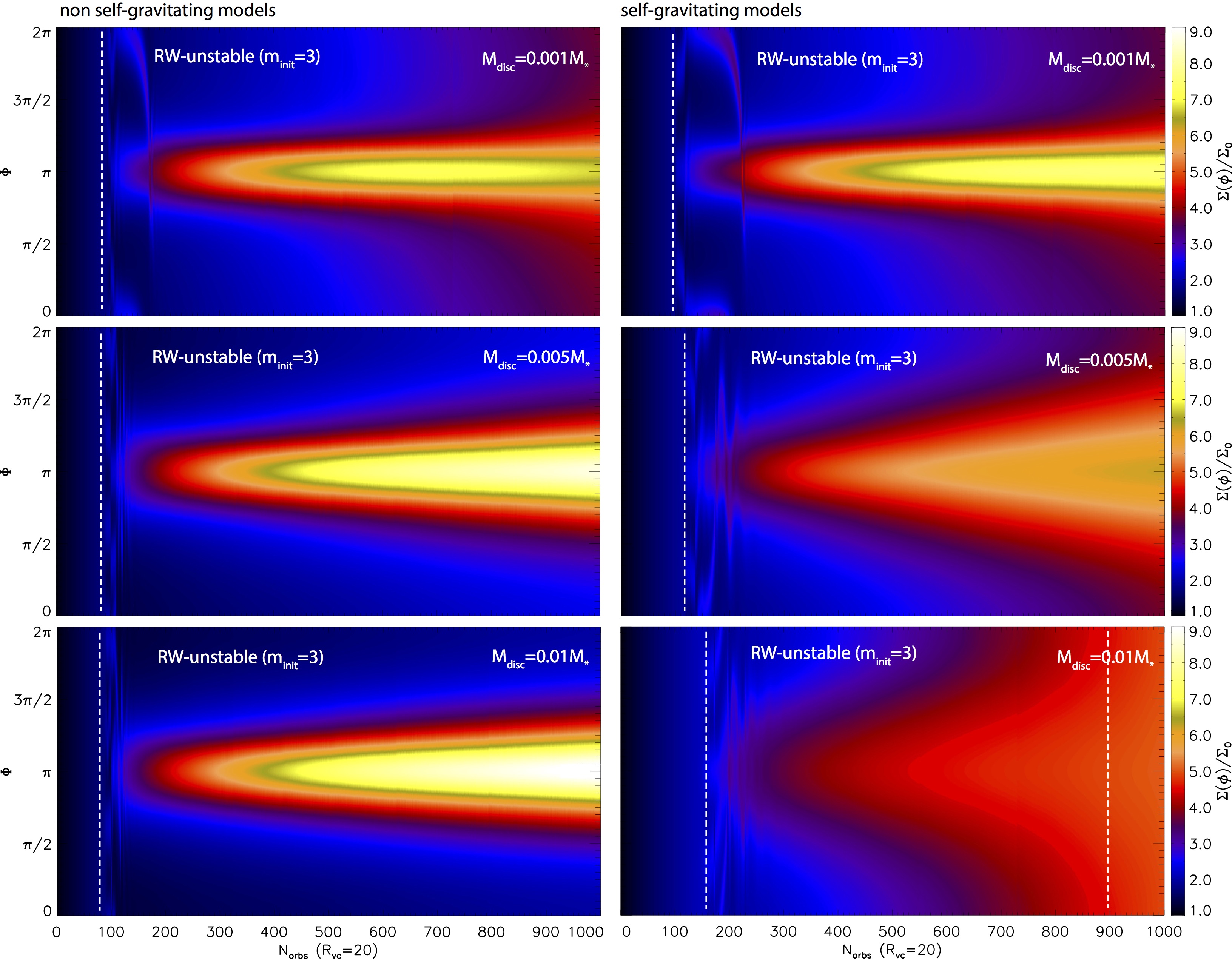 Vortex evolution in models assuming viscosity of αdz10-5 
|
|
To understand the vortex stretching phenomenon, we performed a controlled numerical experiment by taking a non-self-gravitating model and turning on disc self-gravity after the vortex becomes fully developed. The radial distance of the vortex centre is unchanged, but the trailing and leading parts of the vortex wings (with respect to the vortex centre and in the direction of the gas orbital motion) are pulled back and pushed forward, respectively. The vortex stretching and tilting can be explained by the effect of the gravitational torque exerted by the vortex itself. |
|
|
Figure on the left shows the spatial distributions of the gas surface density and gravitational torque at the moment when disc self-gravity is turned on and after the vortex has significantly stretched. Evidently, the leading part of the vortex is characterized by the negative gravitational torque, which removes angular momentum from the gas in the leading wing, forcing its gas parcels to move closer to the star. In a Keplerian disc, it also means that these gas parcels will speed up, effectively stretching the vortex in the forward direction. Conversely, the gravitational torque at the trailing part of the vortex is positive, thus depositing angular moment to the trailing wing and forcing its gas parcels to increase their orbital distance. Since the gas orbital velocity is proportional to R-0.5, the leading and trailing wings of the vortex are receding from each other, i.e. the vortex stretches and gets tilted. Due to this vortex stretching, the azimuthal asymmetry decreases causing the magnitude of the disc's gravitational torque to fall by about an order of magnitude during about 4 orbits. |
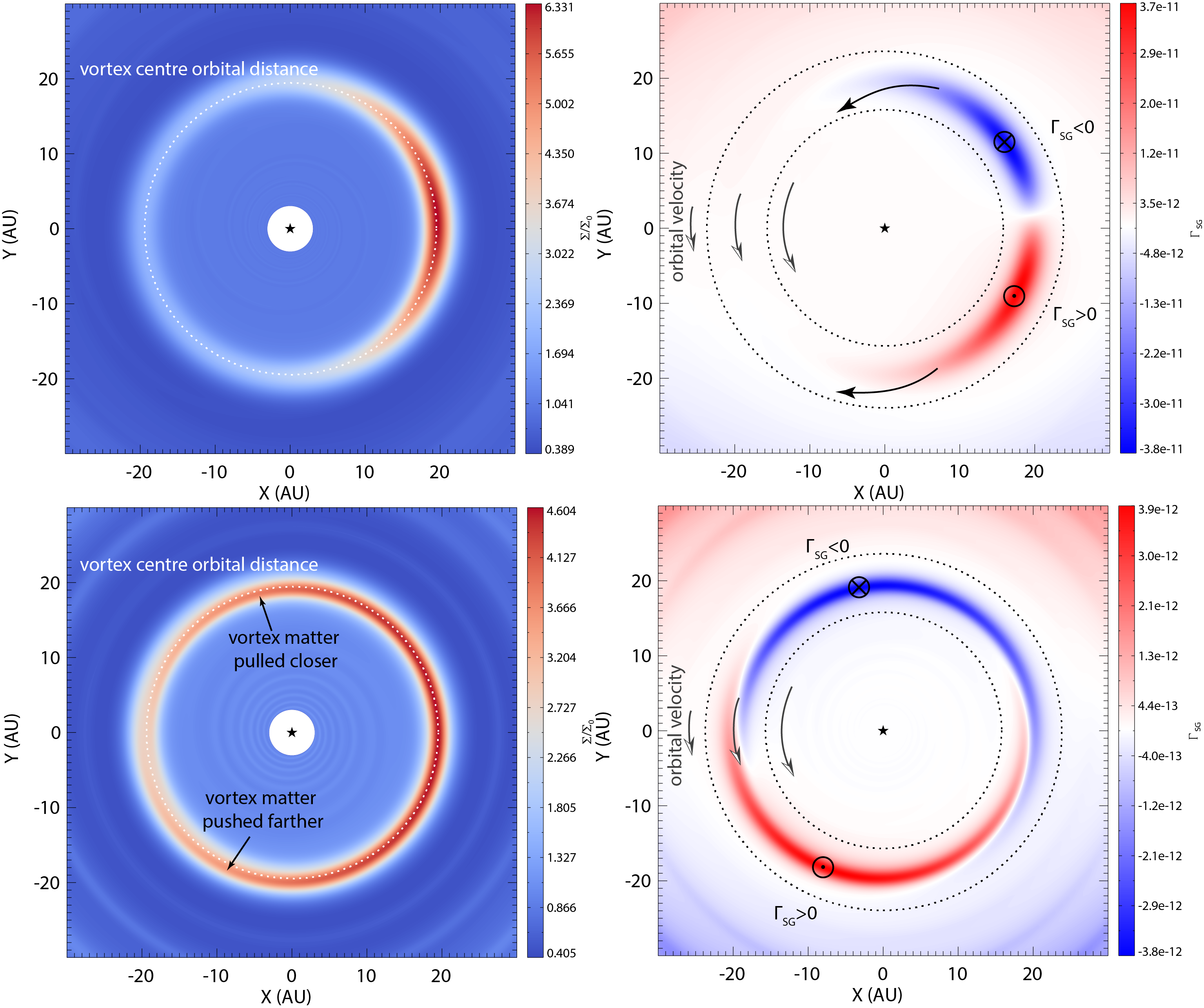 Vortex stretching by its gravitational torque. 
|
|
To summary, we observed a delayed vortex formation and a weaker vortex at a sharp viscosity transition, if disc self-gravity is taken into account similarly to what was found for the gap-edge vortices. Concerning the vortex morphology, we found that the full-fledged vortex becomes azimuthally elongated in self-gravitating discs. The full-fledged vortex is subject to a decay not only due to disc viscosity but also due to disc self-gravity. Moreover, disc self-gravity accelerates the vortex decay as compared to the non-self-gravitating case. The rate of the vortex decay is proportional to the disc mass and becomes significant for Mdisc≥0.005 M∗, where Qinit50 at the vortex radial distance in the unperturbed disc phase. The accelerated vortex decay can be explained by azimuthal stretching of the vortex caused by the vortex's non-vanishing gravitational torque and the Keplerian shear of the disc. Since the magnitude of the vortex gravitational torque is proportional to the disc mass, the vortex lifetime decreases with increasing disc mass. If disc self-gravity is neglected, an opposite correlation is observed between the vortex lifetime and the disc mass, which can be explained by the displacement of the barycentre of the star-disc system caused by the vortex itself (see, e.g., Regaly & Vorobyov 2017). |
Movie of vortex strechning by disc self-gravity. |
|
Large-scale vortices formed at the edges of a gap opened by an embedded planet (Li et al. 2005) or at the edges of the disc's accretionally inactive dead zone (Lovelace et al. 1999; Li et al. 2000) can explain horseshoe-shaped brightness asymmetries observed for several transitional discs (Regaly et al. 2012). The two formation scenarios, however, results in different vortex morphology: while gap edge vortices are azimuthally concentrated, dead zone edge vortices are azimuthally more extended. This phenomenon can be used to infer the vortex formation scenario. Since disc self-gravity tends to increase the vortex azimuthal extension and decrease the azimuthal contrast affecting its dust collection efficiency, it may have a significant effect on the observed brightness asymmetries. According to a previously proposed scenario, large-scale vortices can become gravitationally unstable and collapse to massive planets, although the disc itself may be gravitationally stable (see, e.g., Adams & Watkins, 1995; Lin & Papaloizou 2011). We conclude that this can not be a plausible pathway to planet formation unless the disc is very massive (i.e. gravitationally unstable), because of the vortex stretching caused by disc self-gravity, which tends to decrease the density enhancement at the vortex centre. Another promising planet formation scenario could be the vortex-aided planet formation, wherein vortices behave as planetary cradles by accumulating significant amount of dust. Our results show that this mechanism would favour low-mass and low-viscosity protoplanetary discs, or late phases, when the disc already lost significant amount of its mass. | |
Appeared in Regály, Zs. & Vorobyov, E., 2017, MNRAS, Volume 471, Issue 2, p2204
ADS:2017MNRAS.471.2204R,
arXiv:
Conference poster Planet Formation and Evolution, Jena, 2017: download (A4)

